Recursion trees and the idea behind the Master Theorem

A recursion tree is a helpful way to visualize the time performance of a recursive process.

The figure below shows a simple recursive process. The initial problem has size \(n=8\). We can solve it by dividing into two smaller problems, each one half of the problem. These divisions are applied repeatedly until the resulting smaller problems cannot be divided any further.

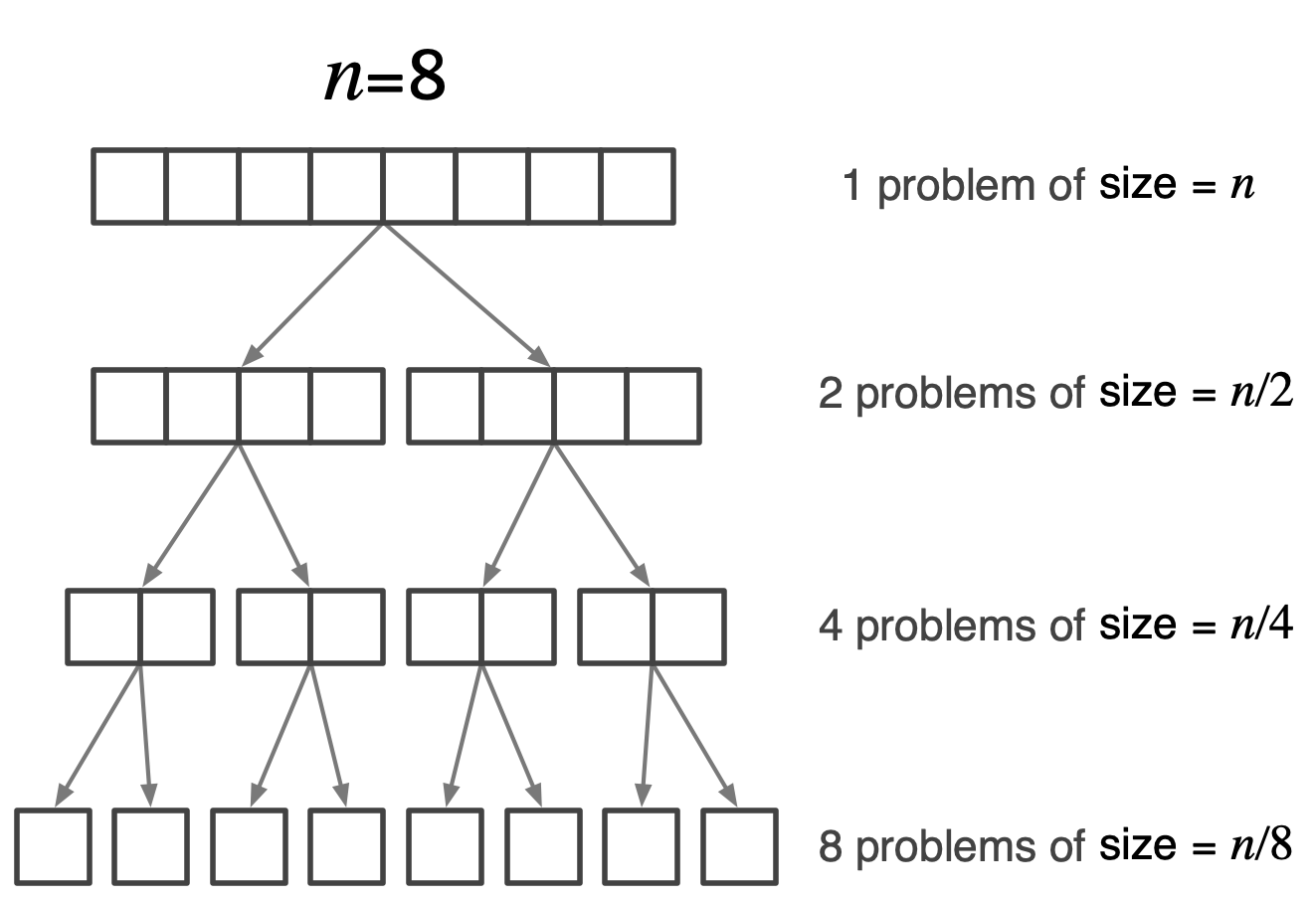
A simple recursion tree with a problem of initial size \(n=8\) divided, repeatedly, into subproblems each scaled by \(1/2\).

Because we are splitting in half, it takes \(\log_2 n\) steps to end up with the smallest possible problems – those whose size is just 1. In this example, we chose an initial size of \(n=8\). The numbers work out nicely because \(\log_2 8 = 3\). It takes three steps to scale down the problem of size 8 to problems of size 1. The hope here is that by the time we get to the smallest problems, we can solve them more easily than the original problem.

Let’s assume that scaling each problem of size \(n\) takes \(f(n)\) steps. In our simple example it happens so \(f(n)=n\). That’s because it takes \(n\) steps to find the middle point of the problem and split it in half. There are problems that may take more (or, rarely, fewer) steps to scale. So in general we assume that scaling requires \(f(n)\) steps.

The time it takes to process the problem of size \(n\) is a function of \(n\):

\[T(n) = 2T\left(\frac{n}{2}\right) + f(n)\]

We already described the term \(f(n)\), so let’s talk a bit about the term \(2T(n/2)\). Splitting the problem of size \(n\) into two smaller problems of size \(n/2\) means that each of these problems will take \(T(n/2)\) time to process further. And because there are two of these smaller problems, they will take \(2T(n/2)\) in total.

The issue now is that we don’t know what \(T(n)\) really looks like. It’s a function of \(n\) that is defined as the value of itself for a smaller argument (\(n/2\)). We are just kicking the can down the road:

\[\begin{split}T(n) = 2&T\left(\frac{n}{2}\right) + f(n) \\ &T\left(\frac{n}{2}\right) = 2T\left(\frac{n}{4}\right) + f\left(\frac{n}{2}\right),\ \text{etc}\end{split}\]

But we can’t keep doing this for ever.

Going from one problem of size 8 to two problems of size 4 will require \(f(8)\) steps. Going from two problems of size 4 to four problems of size 2 will require \(f(4)+f(4)\) steps. Going from four problems of size 2 to eight problems of size 1 will require \(f(2)+f(2)+f(2)+f(2)\). Finally, dealing with the problems of size 1 will require \(f(1)+f(1)+f(1)+f(1)+f(1)+f(1)+f(1)+f(1)\) steps.

The total number of steps \(T(n)\) (using multiplications instead of additions to keep things a bit short), is:

\[\begin{split}T(8) = f(8) + 2f(4) + 4f(2) + 8f(1) \\\end{split}\]

We can write this sum in a compact form, which is more useful that writing \(T(n)\) in terms of \(T(n/2)\) as we attempted earlier.

\[T(n) = \sum_{i=0}^L 2^i f\left(\frac{n}{2^i}\right)\]

Of course we need to know the value of \(L\): how many terms will there be in the sum. Here, \(L=\log_28=3\) and there are four terms to the sum (since we start from \(i=0\)). Why is \(L=\log_2n\), the logarithm, base-2, of the size of the problem? Because if you keep splitting a problem of size \(n\) in half, it will take \(\log_2n\) steps to reduce the size to just 1.

Let’s go back to the sum \(f(8) + 2f(4) + 4f(2) + 8f(1)\). There are three special cases regarding the relation between its terms: the terms can get progressively smaller, the terms are relatively equal, or the terms can get progressively larger.

Progressively smaller terms

If \(f(8) > 2f(4) > 4f(2) > 8f(1)\), it means that the first term dominates the sum. It is fair to assume that for sufficiently large values of \(n\), \(f(n)+2f(n/2)+\ldots\approx f(n)\). The heavy lifting of the recursive process that leads to this behavior is done at the top of the recursion tree. In this case, \(f(n)\) is the upper bound of the sum \(T(n)\). In big-Oh notation, \(T(n)\in\mathcal{O}(f(n))\) or, more confusingly, \(T(n)=\mathcal{O}(f(n))\). (It’s important to remember here that the symbol “=” before a complexity class like light big-oh does not mean “equals”, but that “the function to my left is in the complexity class to my right”).

Approximately equal terms

If \(f(8) \approx 2f(4) \approx 4f(2) \approx 8f(1)\), it means that each term contributes about the same to the process. The sum can be simplified:

\[\begin{split}T(8) &= f(8) + 2f(4) + 4f(2) + 8f(1) \\ &\approx f(8)+f(8)+f(8)+f(8) \\ &=4f(8) \\ &=(1+3)\,f(8) \\ &=(1+\log_28)\,f(8) = (1+\log_2n)\,f(n)\end{split}\]

For sufficiently large values of \(n\) we can assume that \((1+\log_2n)\approx\log_2n\) and therefore \(T(n) \approx \log_2n\,f(n)\). In other words, \(\log_2n\,f(n)\) is the upper bound for the sum and therefore \(T(n) \in\mathcal{O}(\log_{2}{n}\,f(n))\).

Progressively larger terms

If \(f(8) < 2f(4) < 4f(2) < 8f(1)\), it means that the last term dominates the sum. It is fair to assume that for sufficiently large values of \(n\), \(f(n)+2f(n/2)+\ldots\approx 2^{?}f(1)\). All we have to do now is to figure what is the mystery exponent \(2^?\). In the example above, where each problem is scaled down by half, its takes \(\log_2{n}\) splits to go down to the smallest possible problems. From a single problem of size 8, we go down to 2 smaller problems of size 4, then size 2, finally size 1. At the end, there are \(2^{\log_2{n}}\) problems of size 1.

If you remember your logarithms, you might notice that \(2^{\log_2{n}} = n^{\log_22}=n\). Are we doing all this mathematical work to state the obvious? Certainly not. It just so happens that we are dividing the problem size by 2 and we are spawning 2 subproblems. In general we may be dividing the problem size by \(c\) and spawning \(r\) subproblems. In this case there are \(n^{\log_cr}\) problems of the smallest size. It so happens in the simple example we use, that \(c=r=2\) and therefore \(\log_22=1\).

Master Theorem

Earlier, we saw that the if we are splitting a problem into two subproblems of half the size, the time required is:

\[T(n) = 2T\left(\frac{n}{2}\right) + f(n)\]

Others problems may have different solutions. For example, we may be creating 3 subproblems each one fifth of the size. In general, we may be creating \(r\) subproblems, scaled down by a factor of \(1/c\). In this case we can write the recurrence relation – that’s what we call the formula that kicks the can down the road – as:

\[T(n) = r T\left(\frac{n}{c}\right) + f(n)\]

If we write \(T(n/c)\) in terms of the next step:

\[T\left(\frac{n}{c}\right) = r T\left(\frac{n}{c^2}\right) + f\left(\frac{n}{c}\right)\]

and we substitute this in the expression for \(T(n)\) we get:

\[\begin{split}T(n) = & r T\left(\frac{n}{c}\right) + f(n) \\ \\ = & r\underbrace{ \left[r T\left(\frac{n}{c^2}\right) + f\left(\frac{n}{c}\right)\right]}_{T(n/c)} + f(n) \\ \\ = & r^2T\left(\frac{n}{c^2}\right) + rf\left(\frac{n}{c}\right) + f(n)\end{split}\]

Next, if we write \(T(n/c^2)\) as \(rT(n/c^3)+f(n/c^2)\) and substitute above, we get:

\[ \begin{align}\begin{aligned}\begin{split}T(n) = & r^2\underbrace{ \left[r T\left(\frac{n}{c^3}\right) + f(\frac{n}{c^2})\right]}_{T(n/c^2)} + rf\left(\frac{n}{c}\right) + f(n) \\ \\\end{split}\\\begin{split}= & r^3T\left(\frac{n}{c^3}\right) + r^2f(\frac{n}{c^2}) + rf\left(\frac{n}{c}\right) + f(n) \\\end{split}\end{aligned}\end{align} \]

Eventually, we will reach a value \(L\) for which \(n/c^L=1\). At this point we cannot continue scaling the problem by \(1/c\), i.e,. we cannot write that \(T(1) = rT(1/c) +f(1)\). Instead, we reached the point where we can directly solve the problem of size 1 without kicking the proverbial can any further down the road. Here, \(T(1)=f(1)\). And so, the sum for \(T(n)\) can be rewritten as:

\[\begin{split}T(n) & = r^L f\underbrace{\left(\frac{n}{c^L}\right)}_{T(n/c^L)=f(1)} + r^{L-1} f\left(\frac{n}{c^{L-1}}\right) +\ldots + r^2 f(\frac{n}{c^2}) + r f\left(\frac{n}{c}\right) + f(n) \\ \\ & = \sum_{i=0}^L r^i f\left(\frac{n}{c^i}\right) \\\end{split}\]

For \(i=0\), the first term of the sum is just \(f(n)\). When \(i=L\), the last term of the sum is \(r^L f(n/c^L)\). Since \(n/c^L=1\), the last term of the sum is just \(r^Lf(1)\). As we saw earlier, these two terms are important. If the terms of the sum are decreasing monotonically, the first term \(f(n)\) is the dominant term. And if the terms of the sum increase monotonically, the last term \(r^Lf(1)\) dominates.

If the terms of the sum are equal (or equal-ish) to each other, we can write:

\[\begin{split}T(n) & = & \sum_{i=0}^L r^i f\left(\frac{n}{c^i}\right) \\ & =\, & (L+1) f(n) \\ &\approx& L f(n)\end{split}\]

\(L\) is the number of problem reductions we go before we reach the smallest possible problem size. If we start with a problem of size \(n\) and we keep reducing it into smaller problems scaled by \(1/c\), it will take \(\log_cn\) reductions to get there. So \(L=\log_cn\).

Now that we have a fully parametric expression for the time required by the recursion

\[T(n) = r T \left(\frac{n}{c}\right) + f(n)\]

we can look for the conditions that cause the series \(\sum_i r^if(n/c^i)\) to converge, diverge, or remain the same.

Series \(\sum r^if(n/c^i)\) converges

This means that terms are getting progressively smaller. For example we expect the first two terms to be:

\[\begin{split}r^0 f(n/c^0) & > r^1f(n/c^1) \Rightarrow \\ f(n) & > rf(n/c)\end{split}\]

Let’s assume that \(f(n)=n^d\). We can rewrite the inequality as:

\[n^d > rn^d/c^d \Rightarrow 1 > r/c^d \Rightarrow c^d > r\]

In other words, when \(c^d>r\) the heavy lifting in the recurrence is done at the top of the tree.

Series \(\sum r^if(n/c^i)\) diverges

In this case, the terms get progressively smaller. For example we expect the last two terms to be

\[r^{L-1}f(n/c^{L-1}) < r^Lf(n/c^L)\]

Again, let’s assume that \(f(n) = n^d\) and replace it:

\[\begin{split}r^{L-1}n^d/c^{d(L-1)} & < r^Ln^d/c^{dL} \Rightarrow \\ r^{L-1}/c^{d(L-1)} & < r^L/c^{dL} \Rightarrow \\ 1/c^{d(L-1)} & < r/c^{dL} \Rightarrow \\ c^d/c^{dL} & < r/c^{dL} \Rightarrow c^d < r\end{split}\]

When \(c^d<r\), the heavy lifting in the recurrence is done by the bottom of the tree (its leaves).

Series \(\sum r^if(n/c^i)\) is steady

Finally, when each term of the series is the same, we can compare the first two terms:

\[r^0f(n/c^0) = r^1f(n/c^1) \Rightarrow f(n) = rf(n/c)\]

Substituting \(f(n)=n^d\) gives us:

\[n^d = rn^d/c^d \Rightarrow 1 = r/c^d \Rightarrow c^d = r\]

The condition for a steady series is, therefore, \(c^d=r\).

Summarize our findings

The performance of the recurrence

\[T(n) = r T \left(\frac{n}{c}\right) + \underbrace{\mathcal{O}(n^d)}_{f(n)}\]

can be found from

\[\begin{split}T(n) = \begin{cases} \mathcal{O}\left( n^d\log n \right)\ &\text{if}\ r=c^d \\ \mathcal{O}\left( n^d \right)\ &\text{if}\ r < c^d \\ \mathcal{O}\left( n^{\log_cr} \right)\ &\text{if}\ r > c^d \\ \end{cases}\end{split}\]

The expression above is known as the Master Theorem for the standard recurrence.