Recursion trees and the idea behind the Master Theorem

A recursion tree is a helpful way to visualize the time performance of a recursive process.

The figure below shows a simple recursive process. The initial problem has size \(n=8\). We can solve it by dividing into two smaller problems, each one half of the problem. These divisions are applied repeatedly until the resulting smaller problems cannot be divided any further.

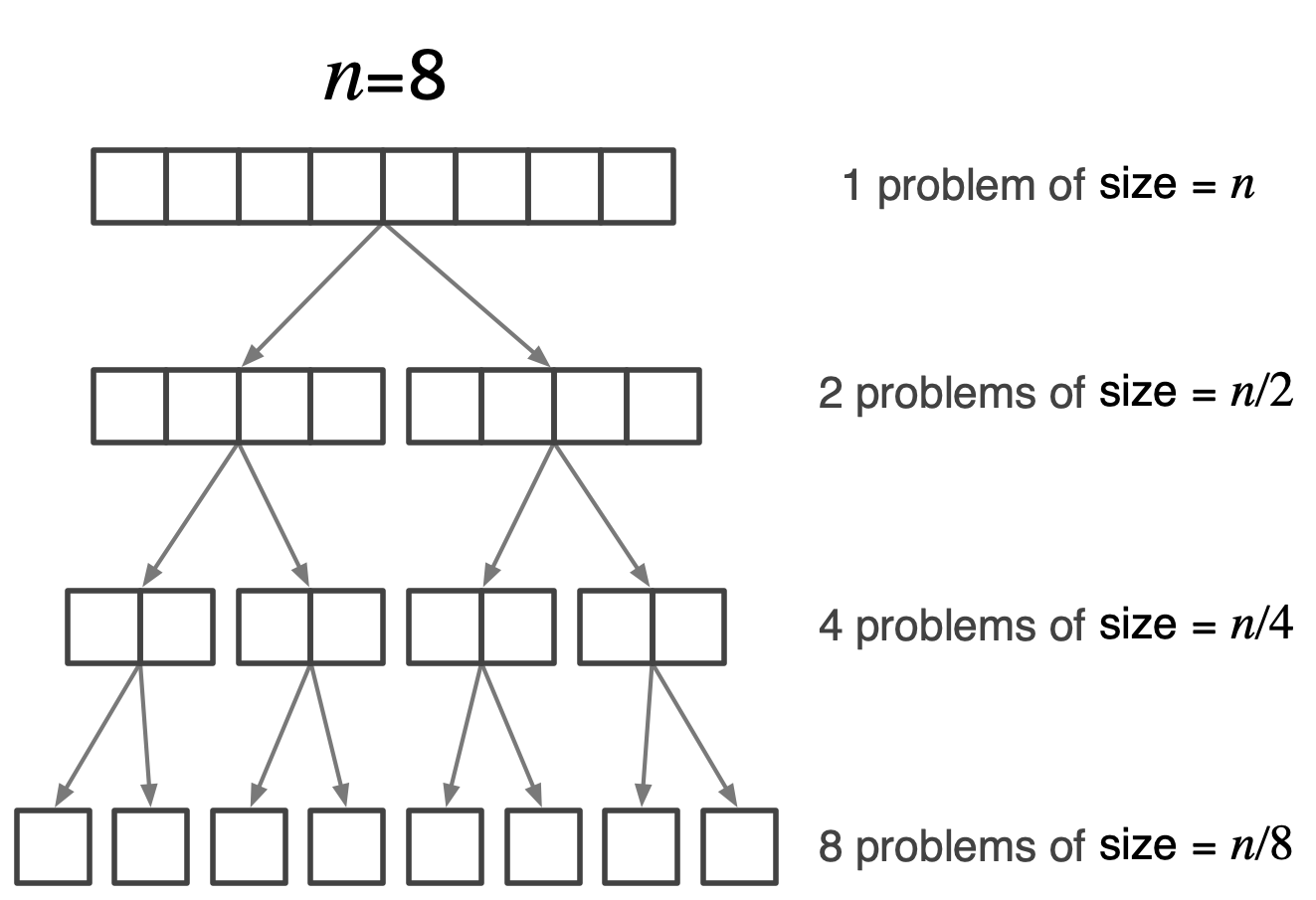
A simple recursion tree with a problem of initial size \(n=8\) divided, repeatedly, into subproblems each scaled by \(1/2\).

Because we are splitting in half, it takes \(\log_2 n\) steps to end up with the smallest possible problems – those whose size is just 1. In this example, we chose an initial size of \(n=8\). The numbers work out nicely because \(\log_2 8 = 3\). It takes three steps to scale down the problem of size 8 to problems of size 1. The hope here is that by the time we get to the smallest problems, we can solve them more easily than the original problem.

An example of such problem is the merge sort technique. It is relatively easy to merge two sorted arrays. And so our goal is to take a larger array, split it down to arrays with single elements which are, by definition sorted, and then start merging those sorted arrays into larger sorted arrays, and so on.

Let’s assume that assemblying the solution of each problem of size \(n\) after we split it into smaller problems, takes \(f(n)\) steps. In the example of merge sort \(f(n)=n\). That’s because it takes approximately \(n\) steps to merge two sorted arrays of size \(n/2\) each. There are problems that may take more (or, rarely, fewer) steps. So in general we assume that combining the smaller solutions requires \(f(n)\) steps.

The time it takes to process the problem of size \(n\) is a function of \(n\):

\[T(n) = 2T\left(\frac{n}{2}\right) + f(n)\]

We already described the term \(f(n)\), so let’s talk a bit about the term \(2T(n/2)\). Splitting the problem of size \(n\) into two smaller problems of size \(n/2\) means that each of these problems will take \(T(n/2)\) time to process further. And because there are two of these smaller problems, they will take \(2T(n/2)\) in total.

The issue now is that we don’t know what \(T(n)\) really looks like. It’s a function of \(n\) that is defined as the value of itself for a smaller argument (\(n/2\)). We are just kicking the can down the road:

\[\begin{split}T(n) = 2&T\left(\frac{n}{2}\right) + f(n) \\ &T\left(\frac{n}{2}\right) = 2T\left(\frac{n}{4}\right) + f\left(\frac{n}{2}\right),\ \text{etc}\end{split}\]

But we can’t keep doing this for ever.

Combining the solution of two smaller problems (of size, say, 4) to the solution of a larger problem, of size 8, will require \(f(8)\) steps.

Combining the solutions of two smaller problems (of size 2) to the solution of a larger problem of size 4, will require \(f(4)\) steps. But we have two of those larger problems to solve, so it will take \(f(4)+f(4)\) steps.

Combining the solutions of two smaller problems (of size 1) to the solution of a larger problem, of size 2, will require \(f(2)\) steps. But since there are four such problems to solve, we’ll need a total of \(f(2)+f(2)+f(2)+f(2)\) steps.

Finally, when we get to solving those size \(n=1\) problems, there is no smaller subproblems to combine. At this level \(f(1)\) is the time to combine these uniquely simple problems. There are eight such problems, and the total time will be \(f(1)+f(1)+f(1)+f(1)+f(1)+f(1)+f(1)+f(1)\) steps.

The total number of steps \(T(n)\) (using multiplications instead of additions to keep the equation short), is:

\[\begin{split}T(8) = f(8) + 2f(4) + 4f(2) + 8f(1) \\\end{split}\]

We can write this sum in a compact form, which is more useful that writing \(T(n)\) in terms of \(T(n/2)\) as we attempted earlier.

\[T(n) = \sum_{i=0}^L 2^i f\left(\frac{n}{2^i}\right)\]

Of course we need to know the value of \(L\): how many terms will there be in the sum. Here, \(L=\log_28=3\) and there are four terms to the sum (since we start from \(i=0\)). Why is \(L=\log_2n\), the logarithm, base-2, of the size of the problem? Because if you keep splitting a problem of size \(n\) in half, it will take \(\log_2n\) steps to reduce the size to just 1.

Let’s go back to the sum \(f(8) + 2f(4) + 4f(2) + 8f(1)\). There are three special cases regarding the relation between its terms: the terms can get progressively smaller, the terms are relatively equal, or the terms can get progressively larger.

Progressively smaller terms

If \(f(8) > 2f(4) > 4f(2) > 8f(1)\), it means that the first term dominates the sum. It is fair to assume that for sufficiently large values of \(n\), \(f(n)+2f(n/2)+\ldots\approx f(n)\). The heavy lifting of the recursive process that leads to this behavior is done at the top of the recursion tree. In this case, \(f(n)\) is the upper bound of the sum \(T(n)\). In big-Oh notation, \(T(n)\in\mathcal{O}(f(n))\) or, more confusingly, \(T(n)=\mathcal{O}(f(n))\). (It’s important to remember here that the symbol “=” before a complexity class like light big-oh does not mean “equals”, but that “the function to my left is in the complexity class to my right”).

Approximately equal terms

If \(f(8) \approx 2f(4) \approx 4f(2) \approx 8f(1)\), it means that each term contributes about the same to the process. The sum can be simplified:

\[\begin{split}T(8) &= f(8) + 2f(4) + 4f(2) + 8f(1) \\ &\approx f(8)+f(8)+f(8)+f(8) \\ &=4f(8) \\ &=(1+3)\,f(8) \\ &=(1+\log_28)\,f(8) = (1+\log_2n)\,f(n)\end{split}\]

For sufficiently large values of \(n\) we can assume that \((1+\log_2n)\approx\log_2n\) and therefore \(T(n) \approx \log_2n\,f(n)\). In other words, \(\log_2n\,f(n)\) is the upper bound for the sum and therefore \(T(n) \in\mathcal{O}(\log_{2}{n}\,f(n))\).

Progressively larger terms

If \(f(8) < 2f(4) < 4f(2) < 8f(1)\), it means that the last term dominates the sum. It is fair to assume that for sufficiently large values of \(n\), \(f(n)+2f(n/2)+\ldots\approx 2^{?}f(1)\). All we have to do now is to figure what is the mystery exponent \(2^?\). In the example above, where each problem is scaled down by half, its takes \(\log_2{n}\) splits to go down to the smallest possible problems. From a single problem of size 8, we go down to 2 smaller problems of size 4, then size 2, finally size 1. At the end, there are \(2^{\log_2{n}}\) problems of size 1.

If you remember your logarithms, you might notice that \(2^{\log_2{n}} = n^{\log_22}=n\). Are we doing all this mathematical work to state the obvious? Certainly not. It just so happens that we are dividing the problem size by 2 and we are spawning 2 subproblems. In general we may be dividing the problem size by \(c\) and spawning \(r\) subproblems. In this case there are \(n^{\log_cr}\) problems of the smallest size. It so happens in the simple example we use, that \(c=r=2\) and therefore \(\log_22=1\).

Master Theorem

Earlier, we saw that the if we are splitting a problem into two subproblems of half the size, the time required is:

\[T(n) = 2T\left(\frac{n}{2}\right) + f(n)\]

Others problems may have different solutions. For example, we may be creating 3 subproblems each one fifth of the size. In general, we may be creating \(r\) subproblems, scaled down by a factor of \(1/c\). In this case we can write the recurrence relation – that’s what we call the formula that kicks the can down the road – as:

\[T(n) = r T\left(\frac{n}{c}\right) + f(n)\]

If we write \(T(n/c)\) in terms of the next step:

\[T\left(\frac{n}{c}\right) = r T\left(\frac{n}{c^2}\right) + f\left(\frac{n}{c}\right)\]

and we substitute this in the expression for \(T(n)\) we get:

\[\begin{split}T(n) = & r T\left(\frac{n}{c}\right) + f(n) \\ \\ = & r\underbrace{ \left[r T\left(\frac{n}{c^2}\right) + f\left(\frac{n}{c}\right)\right]}_{T(n/c)} + f(n) \\ \\ = & r^2T\left(\frac{n}{c^2}\right) + rf\left(\frac{n}{c}\right) + f(n)\end{split}\]

Next, if we write \(T(n/c^2)\) as \(rT(n/c^3)+f(n/c^2)\) and substitute above, we get:

\[ \begin{align}\begin{aligned}\begin{split}T(n) = & r^2\underbrace{ \left[r T\left(\frac{n}{c^3}\right) + f(\frac{n}{c^2})\right]}_{T(n/c^2)} + rf\left(\frac{n}{c}\right) + f(n) \\ \\\end{split}\\\begin{split}= & r^3T\left(\frac{n}{c^3}\right) + r^2f(\frac{n}{c^2}) + rf\left(\frac{n}{c}\right) + f(n) \\\end{split}\end{aligned}\end{align} \]

Eventually, we will reach a value \(L\) for which \(n/c^L=1\). At this point we cannot continue scaling the problem by \(1/c\), i.e,. we cannot write that \(T(1) = rT(1/c) +f(1)\). Instead, we reached the point where we can directly solve the problem of size 1 without kicking the proverbial can any further down the road. Here, \(T(1)=f(1)\). And so, the sum for \(T(n)\) can be rewritten as:

\[\begin{split}T(n) & = r^L f\underbrace{\left(\frac{n}{c^L}\right)}_{T(n/c^L)=f(1)} + r^{L-1} f\left(\frac{n}{c^{L-1}}\right) +\ldots + r^2 f(\frac{n}{c^2}) + r f\left(\frac{n}{c}\right) + f(n) \\ \\ & = \sum_{i=0}^L r^i f\left(\frac{n}{c^i}\right) \\\end{split}\]

For \(i=0\), the first term of the sum is just \(f(n)\). When \(i=L\), the last term of the sum is \(r^L f(n/c^L)\). Since \(n/c^L=1\), the last term of the sum is just \(r^Lf(1)\). As we saw earlier, these two terms are important. If the terms of the sum are decreasing monotonically, the first term \(f(n)\) is the dominant term. And if the terms of the sum increase monotonically, the last term \(r^Lf(1)\) dominates.

If the terms of the sum are equal (or equal-ish) to each other, we can write:

\[\begin{split}T(n) & = & \sum_{i=0}^L r^i f\left(\frac{n}{c^i}\right) \\ & =\, & (L+1) f(n) \\ &\approx& L f(n)\end{split}\]

\(L\) is the number of problem reductions we go before we reach the smallest possible problem size. If we start with a problem of size \(n\) and we keep reducing it into smaller problems scaled by \(1/c\), it will take \(\log_cn\) reductions to get there. So \(L=\log_cn\).

Now that we have a fully parametric expression for the time required by the recursion

\[T(n) = r T \left(\frac{n}{c}\right) + f(n)\]

we can look for the conditions that cause the series \(\sum_i r^if(n/c^i)\) to converge, diverge, or remain the same.

Sum \(\sum r^if(n/c^i)\) has decreasing terms.

This means that terms are getting progressively smaller. For example we expect the first two terms to be:

\[\begin{split}r^0 f(n/c^0) & > r^1f(n/c^1) \Rightarrow \\ f(n) & > rf(n/c)\end{split}\]

Let’s assume that \(f(n)=n^d\). We can rewrite the inequality as:

\[n^d > rn^d/c^d \Rightarrow 1 > r/c^d \Rightarrow c^d > r\]

In other words, when \(c^d>r\) the heavy lifting in the recurrence is done at the top of the tree.

Sum \(\sum r^if(n/c^i)\) has increasing terms

In this case, the terms get progressively larger. For example we expect the last two terms to be

\[r^{L-1}f(n/c^{L-1}) < r^Lf(n/c^L)\]

Again, let’s assume that \(f(n) = n^d\) and replace it:

\[\begin{split}r^{L-1}n^d/c^{d(L-1)} & < r^Ln^d/c^{dL} \Rightarrow \\ r^{L-1}/c^{d(L-1)} & < r^L/c^{dL} \Rightarrow \\ 1/c^{d(L-1)} & < r/c^{dL} \Rightarrow \\ c^d/c^{dL} & < r/c^{dL} \Rightarrow c^d < r\end{split}\]

When \(c^d<r\), the heavy lifting in the recurrence is done by the bottom of the tree (its leaves).

Sum \(\sum r^if(n/c^i)\) has equal terms

Finally, when each term of the series is the same, we can compare the first two terms:

\[r^0f(n/c^0) = r^1f(n/c^1) \Rightarrow f(n) = rf(n/c)\]

Substituting \(f(n)=n^d\) gives us:

\[n^d = rn^d/c^d \Rightarrow 1 = r/c^d \Rightarrow c^d = r\]

The condition for a steady series is, therefore, \(c^d=r\).

Summarize our findings

The performance of the recurrence

\[T(n) = r T \left(\frac{n}{c}\right) + \underbrace{\mathcal{O}(n^d)}_{f(n)}\]

can be found from

\[\begin{split}T(n) = \begin{cases} \mathcal{O}\left( n^d\log n \right)\ &\text{if}\ r=c^d \\ \mathcal{O}\left( n^d \right)\ &\text{if}\ r < c^d \\ \mathcal{O}\left( n^{\log_cr} \right)\ &\text{if}\ r > c^d \\ \end{cases}\end{split}\]

The expression above is known as the Master Theorem for the standard recurrence.